МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ, ИСПОЛЬЗУЕМЫЕ В СОВРЕМЕННЫХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЯХ СИСТЕМ УПРАВЛЕНИЯ
Достоинства цифровых методов представления, обработки, передачи и хранения информации, бурное развитие элементной базы - все это способствует тому, что цифровые методы обработки и передачи информации стали основным направлением развития телекоммуникационных систем. Эффективность методов цифровой обработки сигналов (ЦОС), составляющих основу многих ИТ, полностью определяется математической моделью ЦОС.
Существующая в последние годы тенденция в цифровой вычислительной технике к распараллеливанию вычислений связана с непрерывным ростом требований к производительности вычислительных устройств ЦОС.
Однако предъявляемые жесткие временные ограничения и отсутствие высокопроизводительной нейросетевой базы ЦОС является основным сдерживающим фактором широкого внедрения методов цифрового преобразования сигналов в системах передачи речи со сжатием, статистическим уплотнением, пакетной коммутацией, IP-телефонии и других инфотелекоммуникационных системах.
При анализе сигналов и цифровых методах их обработки особое внимание привлекают ортогональные преобразования благодаря простоте вычисления координат разлагаемых функций в прострaнcтве. Такие преобразования определены над полем комплексных чисел,
где - поворачивающий коэффициент;
x(n)- количество отсчетов, k=0,...,N-1, n=0,...,N-1.
Известно, что реализация прямого и обратного ДПФ предопределяет значительные погрешности при вычислении значений спектральных коэффициентов в поле комплексных чисел. С этой точки зрения наиболее привлекательными являются преобразования, определенные над расширенным полем Галуа GF(pv). Так как элементы поля представляют собой целочисленные элементы расширенного поля Галуа, то при реализации выражений (1) и (2 будут полностью отсутствовать шумы округления [1-3].
Рассмотрим возможность выполнения обобщенного ДПФ в расширенных полях Галуа с использованием конечных полиномиальных колец, полученных с помощью неприводимых полиномов.
Пусть имеем конечное кольцо полиномов P(z), с коэффициентами в виде элементов поля GF(p), определяющего точность вычисления ортогональных преобразований сигналов. Положим, что данное кольцо разлагается в виде P(z) = P1(z) + P2(z) +...+ Pk(z), где P1(z) - локальное кольцо полиномов, образованных неприводимым полиномом pl(z) над полем GF(p); l=1, ...,k. Тогда справедлива теорема.
Теорема: Пусть P(z) - конечное кольцо полиномов с коэффициентами поля GF(p) представляет собой прямую сумму локальных колец полиномов
P(z) = P1(z) + P2(z) +...+ Pm(z),
Тогда в данной системе существует ортогональное преобразование, представляющее собой обобщенное ДПФ, если выполняются следующие условия:
- β 1(z) - первообразный элемент порядка d для локального кольца p1(z), где l=1, ...,m.
- d имеет мультипликативный обратный элемент d*.
Доказательство: Ортогональное преобразование является обобщенным ДПФ для кольца вычетов P(z) если существуют преобразования вида
над конечным кольцом p 1(z).
Полученная циклическая группа имеет порядок d. Поэтому дискретное преобразование Фурье над p1 (z) можно обобщить над кольцом P(z), если конечное кольцо p1 (z) содержит корень d-ой степени из единицы и d имеет мультипликативный обратный элемент d*, такой что справедливо
d*d=pv-1. (5)
Доказательство закончено.
Основным преимуществом теоремы является возможность организации ортогональных преобразований сигналов на основе обобщенного ДПФ в расширенных полях Галуа при различных значениях разрядности сетки, задаваемой значением конечного кольца P(z). При этом вычисления организуются параллельно, независимо друг от друга, что значительно повышает быстродействие ЦОС.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Калмыков И.А. Математические модели нейросете-вых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с
- Калмыков И.А., Чипига А.Ф. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности/Вестник Ставропольского Государственного Университета,2004, Выпуск №38 с.46-50.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.
Работа представлена на заочную научную электронную конференцию «Современные проблемы науки и образования» 15-20 ноября 2008 г. Поступила в редакцию 13.01.09
 Статья в формате PDF
141 KB...
Статья в формате PDF
141 KB...
25 04 2024 4:38:28
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
24 04 2024 13:57:22
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
23 04 2024 16:15:42
22 04 2024 15:19:47
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
21 04 2024 5:59:38
20 04 2024 14:12:31
 Статья в формате PDF
268 KB...
Статья в формате PDF
268 KB...
18 04 2024 3:54:59
 Статья в формате PDF
172 KB...
Статья в формате PDF
172 KB...
17 04 2024 8:27:38
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
16 04 2024 1:14:21
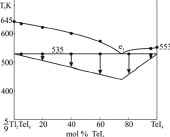 Методами ДТА и РФА исследованы фазовые равновесия в системе Tl2S-Tl2Te-Tl9SbTe6 (А). Построены политермическое сечение Tl2S-Tl9SbTe6 и изотермическое сечение при 400К фазовой диаграммы, а также проекция поверхности ликвидуса системы А. Установлено, что она является квазитройным фрагментом четверной системы Tl-Sb-S-Te и хаpaктеризуется образованием широких областей твердых растворов на основе исходных соединений. Поверхность ликвидуса системы А состоит из трех полей, отвечающих первичной кристаллизации твердых растворов на основе соединений Tl2S, Tl2Te и Tl9SbTe6. В работе также обсуждены особенности фазовых равновесий в аналогичных системах и, в частности, показано, что все шесть систем данного типа хаpaктеризуются образованием твердых растворов на основе исходных соединений, причем наиболее широкие области гомогенности имеют соединения типа Tl9BVX6.
...
Методами ДТА и РФА исследованы фазовые равновесия в системе Tl2S-Tl2Te-Tl9SbTe6 (А). Построены политермическое сечение Tl2S-Tl9SbTe6 и изотермическое сечение при 400К фазовой диаграммы, а также проекция поверхности ликвидуса системы А. Установлено, что она является квазитройным фрагментом четверной системы Tl-Sb-S-Te и хаpaктеризуется образованием широких областей твердых растворов на основе исходных соединений. Поверхность ликвидуса системы А состоит из трех полей, отвечающих первичной кристаллизации твердых растворов на основе соединений Tl2S, Tl2Te и Tl9SbTe6. В работе также обсуждены особенности фазовых равновесий в аналогичных системах и, в частности, показано, что все шесть систем данного типа хаpaктеризуются образованием твердых растворов на основе исходных соединений, причем наиболее широкие области гомогенности имеют соединения типа Tl9BVX6.
...
15 04 2024 6:43:33
14 04 2024 4:43:18
 Статья в формате PDF
250 KB...
Статья в формате PDF
250 KB...
13 04 2024 0:41:44
 Статья в формате PDF
172 KB...
Статья в формате PDF
172 KB...
10 04 2024 0:57:18
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
09 04 2024 7:46:57
 Статья в формате PDF
275 KB...
Статья в формате PDF
275 KB...
08 04 2024 4:34:36
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
07 04 2024 4:58:34
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
06 04 2024 18:14:37
 Статья в формате PDF
323 KB...
Статья в формате PDF
323 KB...
05 04 2024 23:55:33
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
04 04 2024 9:16:43
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
03 04 2024 12:23:59
Статья в формате PDF 101 KB...
30 03 2024 13:25:44
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
29 03 2024 5:44:26
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
27 03 2024 14:44:12
 Статья в формате PDF
275 KB...
Статья в формате PDF
275 KB...
26 03 2024 1:28:25
25 03 2024 22:55:33
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
24 03 2024 12:41:11
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
23 03 2024 15:29:59
Статья в формате PDF 250 KB...
22 03 2024 11:18:59
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
21 03 2024 8:49:28
 Статья в формате PDF
128 KB...
Статья в формате PDF
128 KB...
20 03 2024 21:20:36
Статья в формате PDF 103 KB...
19 03 2024 16:49:39
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
18 03 2024 1:41:57
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
17 03 2024 21:41:43
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::